환영합니다, Rolling Ress의 카루입니다.
눈이 아파요.
target data에 둘 이상의 클래스가 포함된 것을 다중 분류(multiclass classification)라고 한다.


이것은 시그모이드 함수의 함수식이다. 수학시간에 노가다를 뛰었던... 그래프를 보면 알겠지만, 시그모이드 함수는 다음과 같은 성질을 갖는다.

이 함수는 양 끝 값(이란 건 없지만, 그래프에서 직관적으로 볼 수 있듯이)이 0과 1에 각각 수렴한다. 즉, 모든 실수를 0과 1 사이에 대응시킬 수 있다는 의미이다. 어쩌면 이걸 가지고 전체 실수의 개수와 (0, 1)의 실수의 개수가 같다는 걸 증명해도 되긴 하겠다. 뭐...그래. 아무튼, 치역이 (0, 1)이므로 (극한값까지 잘 응용한다면) 0~100%의 확률을 추출하는 데에도 사용할 수 있다.
경사하강법
확률적 경사하강법은 train set에서 랜덤하게 하나의 샘플을 골라 조금씩 훈련하는 것이다. 전체 샘플을 모두 사용할 때까지 계속하며, 하강이 끝나지 않은 경우(1 에포크(=주기) 완료시) 처음부터 다시 시작한다. 미니배치 경사 하강법은 여러 개의 샘플을 사용하는 것이고, 배치 경사 하강법은 모든 샘플을 사용한다.
무엇을 따라 하강하는가? 바로 손실함수(loss function)이다. 손실 함수는 머신러닝의 부정확도를 측정한다. 즉, 함숫값이 낮을 수록 좋다. 이때, 경사하강법에서는 손실 함수를 타고 조금씩 내려온다고 했다. 조금씩. 즉, 손실함수는 미분 가능해야 한다. 그 말은 연속적임을 내포하고 있고, 첨점이 없어야 한다는 뜻이다.
손실 함수를 계산할 때는 predict와 target을 이용한다. 그냥 predict × target × (-1)을 하면 적당한 음수가 나온다. target이 양성 클래스(1)가 아니라 음성 클래스(0)라면, target을 1로 바꿔주고 predict는 1에서 predict를 뺀 값을 사용한다. 이 수들의 크기가 클수록 (절댓값이 작을수록) 손실이 크다. 이때, log함수를 사용한다면 양수와 음수를 뒤집고, 손실을 더욱 크게 만들 수 있다.

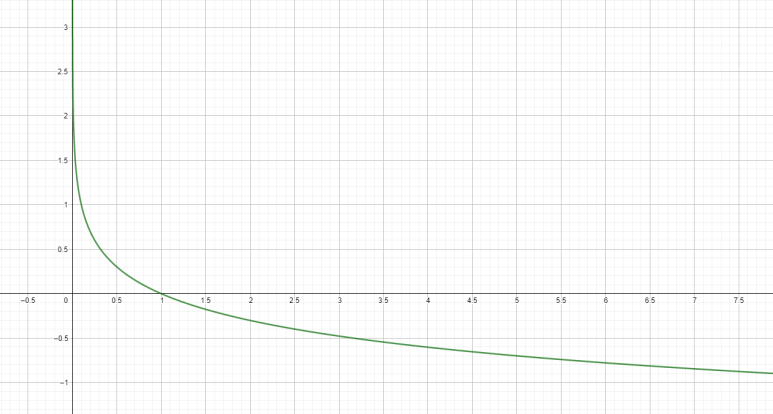
이것을 로지스틱 손실 함수라고 한다. 다른 이름은 Binary Cross-Entropy Loss Function. 다중 분류는 여기서 Binary만 제거한 Cross-Entropy Loss Function을 사용한다.
에포크를 반복하되, overfitting이 일어나기 전에 조기 종료를 해야 한다.

파란색이 train set의 정확도, 주황색이 test set의 정확도입니다. 수치가 보이지는 않는데 대략 90 정도에 둘의 폭이 가장 적은 모습을 볼 수 있어요. 참고로 왼쪽 부분은 생각하지 않습니다. 저긴 underfitting 구간이에요.
'머신러닝 & 딥러닝' 카테고리의 다른 글
| 머신러닝&딥러닝 기초(6): 처음 만드는 인공신경망 (0) | 2022.02.17 |
|---|---|
| 머신러닝&딥러닝 기초(5): 결정 트리, 교차 검증과 그리드 서치, 앙상블 (0) | 2022.02.17 |
| 머신러닝&딥러닝 기초(3): 회귀분석 (0) | 2022.02.15 |
| 머신러닝&딥러닝 기초(2): 머신러닝의 학습과 편향 (0) | 2022.02.13 |
| 머신러닝&딥러닝 기초 (1): 머신러닝 기초를 배우며... (0) | 2022.02.13 |